Derivasjon er en operasjon i matematikk der en bestemmer den deriverte av en funksjon. For en funksjon av én variabel f(x) er den deriverte definert ved

,

dersom grenseverdien eksisterer. Den deriverte er et mål for endringen i funksjonsverdier f(x) når den frie variabelen x endres. Geometrisk er den deriverte et uttrykk for stigningstallet til tangenten til funksjonen.

Video

Den deriverte av en funksjon beskriver hvor raskt funksjonen er i ferd med å forandre seg i et gitt punkt. Derivasjon er et mål for endringen til funksjonsverdien  når -verdi endrer med en veldig liten verdi. Endringsrate/Vekstrate

Gjennomsnittlig og momentan vekstrate(oppgaver , fasit)

En funksjon er deriverbar i et punkt dersom funksjonen er definert i   og grenseverdien ekisterer.

En funksjon som er definert i et lukket intervall, er ikke deriverbar i ende punktene.

En funksjon som har knekkpunkt er ikke deriverbar i knekkpunkt.

Deriverbarhet og knekkpunkt    Video

En funksjon er deriverbar på et intervall dersom funksjonen er deriverbare i alle punkt i og grenseverdiene og eksisterer.

Derivasjonsformler og regler     Oppgaver   fasit

Derivasjonsmetoder

Logaritmisk derivasjon: For å derivere funksjoner som , og , kan vi ta logaritmer på begge sider og deretter deriverer med å bruke produktreglen/kjerneregelen:

, ved å ta "ln" på begge sider:    og ved å derivere:   og dermed

.

, ved å ta "ln" på begge sider:  og ved å derivere:  og dermed

.

, ved å ta "ln" på begge sider:  og ved å derivere:  og dermed

 

Implisitt derivajson

Anvendelser

1) Stigningstallet til tangenten og tangentlinjen

2) Lineær tilnærming - Lineær approksimasjon(video)

3) Newtonsmetode

4) Funksjonsdrøfting     Quiz

Ekstremalpunkt og terassepunkt

Vendepunkt

5) L'Hôpitals regel (L'Hôpitals regel (Lisa Lorentzen/NTNU))

Regelen kan benyttes:

I noen tilfeller som , kan man bruke triks:  (se eksempel 5 i linken nede)

1. Eksempler med fasit
2. Eksempler med fasit ( kan omformes med å ta fra uttrykket, men det ikke vektlagt i pensum)

Tekstoppgaver

6) Fartskoblede oppgaver (Koblede hastigheter (Lisa Lorentzen/NTNU))

Eksempel 1  Stigen faller - video

Eksempel 2 Hastigheten til to biler

Eksempel 3  Vann renner fra kjeglen

Eksempel 4 Hastigheten til skyggen til en fugl

7) Optimeringsoppgaver  - Notater

Lokale og globale ekstremalpunkter (Lisa Lorentzen/NTNU)

Eksempel 1(video) - Å bestemme eventuelle globale og lokale ekstremalpunkt

Eksempel 2 (video)- Bestem og høyden for en sylinder med volum 1000 som gir største overflate areal.

Eksempel 2 (video) - kommer mer.

Flere eksempler

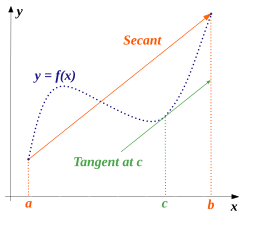
8) Middelverditeorem(sekant setningen) - Video(Teori og eksempel)

Hvis en funksjon $f$ er kontinuerlig på og deriverbare på , fins da et punkt i intervallet slik at:

.

Med andre ord, det finnes et punkt på grafen der tangenten er parrallell med sekanten fra punktet til .

 

9) Taylor polynom av n-te grad til i :

Eksempel: Taylorrekken til i .