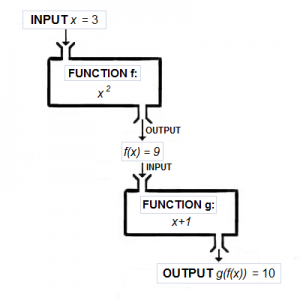
Relasjoner og funksjoner 
Relasjon kan beskrive sammenheng mellom to objekter.
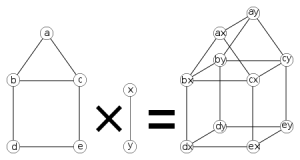
Relasjon er en regel 
som tilordner et element fra en mengde 
til et element i en annen mengde 
og kan defineres ved Kartesisk produkt:
Eksempel 1: 
Eksempel 2:
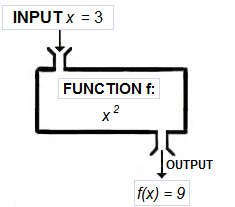
Hva er en funksjon?
I barneskolen møter barna 
og sender i ungdomsskolen lærer elevene om arealet til trekanten og volumet til sylinderen. På videregåendeskole lærer elevene om potenser, logaritmer, trigonometriske funksjoner.
En funksjon 
er en relasjon som tilordner et element(uavhengig variabel) fra en mengde kalt definisjonsmengden(
) til et element i en annen mengde(avhengig variabel) kalt verdimengden(
) og kan defineres ved:
For alle 
finnes det en og bare en 
.
Eksempel 3: 
Viktige begrep
- Injetkiv (en-entydige funksjoner): Til et hvert element i verdimengden finnes bare og bare et element i definisjonsmengden.
- Surjektiv: En funksjon
er surjektiv på dersom til et hvert 
finnes minst ett element 
, slik at 
. Det vil si bildemengden til er alle elementene i . - Bijektiv: En funksjon som er surjektiv og en-entydig.
For eksempel 
er bijektiv.
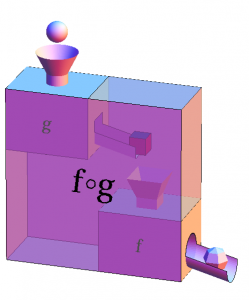
Arealet til en sirkel er gitt ved funksjonen 
. Hvis radien radiusen endrer seg med tiden, har vi en sammensatt funksjon: 
.
En sammensatt funksjon er en funksjon som tar inn en annen funksjon i seg. I den sammensatt funksjonen 
kaller vi den ytre funksjonen og 
indre funksjonen (indre argument).
Her finner du mer om funksjoner (forkurs kompendium) og følgende tema.
Det er veldig viktig å kunne
7) Kjente funksjoner
| Eksempel | Video | Notat | Oppgaver | |
Lineære funksjoner  |
eksempel | Video | Quiz | |
Andre gradsfunksjoner  |
Eks. 1 , eks. 2 | Notat | Quiz | |
| Polynom funksjoner | eksempel | Quiz | ||
Rasjonale funksjoner  |
Eks. 1, Eks. 2 | Quiz | ||
| Potensfunksjoner | Eksempel | Video | Quiz | |
| Eksponentialfunksjoner | Eksempel | kontrolloppgaver m/fasit | ||
| Logaritmer og Logaritmefunksjoner | Eksempel | Video | Notat | kontrolloppgaver m/fasit |
| Trigonometriske funksjoner | Eksempel | Video | Notat | Oppgaver m/fasit |
| Inverse trigonometriske funksjoner | Eksempel | Notat | ||
| Absoluttverdi funksjoner | Eksempel | Video |
Det er også viktig å kunne:
8) Grenseverdi
Vi skal hovedsakelig se på to tilfeller:
- Dersom
går mot et fast tall når 
går mot uendelig, har grafen en horisontal asymptote: 
- Dersom går mot uendelig når går mot et fast tall, har grafen en vertikal asymptote:
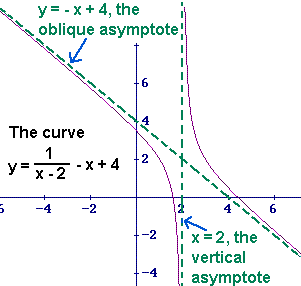
- Dersom går mot en linje, , når går mot uendelig, har grafen en skrå asymptote:
.
Eksempel (Skrå asymptote)
9) Kontinuitet
En funksjon er kontinuerlig i punktet 
dersom grenseverdien i dette punktet er samme som funksjonsverdien i punktet.
.
10) Skjæringssetningen og maksima, minima
--------------------------------------
11) Relasjonsegenskaper
Hvis du vil, kan du les mer om:
En relasjon 
definert ved: 
, der 
og 
:
- Symmetrisk når:
Egenskapen at hvis er relatert til 
, så må være relatert til .
- Refleksiv:
Egenskapen at ethvert element er relatert til seg selv.
- Transitiv når:
Egenskapen at hvis er relatert til og er relatert til 
, så er relatert til .
- Total:
Egenskapen at et element er relatert il eller er relatert til (eller begge).
Denne relasjonen forutsetter refleksivitet.