Integrasjon

I matematikken studeres et objekt ved først å dele det opp i små biter ved derivasjon( kan beskrive stigningstallene til tangentene til hvert punkt på kurven) og deretter å sette dem sammen igjen ved integrasjon:  .

 

Integrasjon handler om å bestemme antideriverte til en kontinuerlig funksjon .

, der er den antideriverte til og dermed .

Areal som integral (Riemann sum)  - Video

Steglengde:

Punktene på -aksen kan da uttrykkes ved

eller

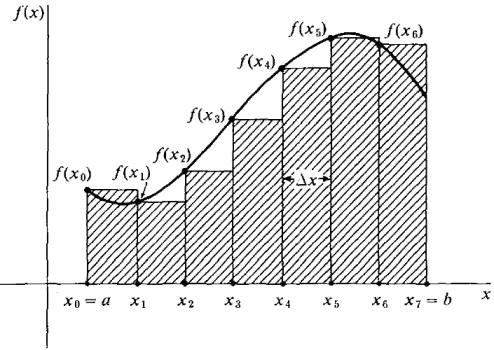Hvis går mot uendelig, kan man fortsette til (øvre indeksen i summen)

 

 

 

 

 

 

Integrasjontabell for enkle integraler

Linearitet egenskapen:

Integrasjonsmetoder  

Det finnes flere integrasjonsmetoder der man bruker variabelskifte eller algebraiske metoder for å gjøre integralet enklere å integrere. I noen oppgaver kan blande disse metode eller bruke flere metoder for å integrere.

Det er veldig viktig er at du ser() grundig på integranden før du begynner å integrere, og bruker dine tidligere erfaringer til å velge metode. Det er også viktig at når du er ferdig med en oppgave, du tar et tilbakeblikk og tar med meg erfaringen for denne oppgaven. Erfaringene dine hjelper deg å velge riktige metoder.

Enkle oppgaver Oppgaver  Fasit

1) Substitusjon Notater  Notater med eksempler    Video

Substitusjon eller variabelskifte er metode der et uttrykk i integranden erstattes med en hjelpevariabel og erstattes med . Hensikten er at den nye integralet er lettere å integrere. Substitusjon kan benyttes blant annet for følgende eksempler:

med

med 

med

med

Trigonometriske substitusjoner  Video

Nevneren  er andre gradspolynom uten reelle løsninger	og prøver å skrive denne som    Legg merke til
	og ved substitusjon får man . Legg merke til:
	Hvis integranden består av bare - eller bare -ledd, eller begge, med partall eksponenter bruker man "dobbelvinkel" fôrmelene:  Bruk og .
	Bruk og
	Hvis integranden består av bare - eller bare -ledd, eller begge, med oddetall eksponenter, faktoriserer man som gir utgangspunkt for å bruke substitusjon med .

   (nevneren er andre gradspolynom med ingen reelle løsninger)

Løsning:

Hjelperegninger:  ,   gir

Triks: Fullstendige kvadrater: 

  

 2) Delvis integrasjon  Notater med eksempler

I vårt pensum brukes delvis integrasjon stortsett når integranden består av:

Polynom eksponential funksjon

Polynom Sinus

Polynom Cosinus

Polynom logaritme funksjoner

Delvis integrasjon kan også benyttes for integraler som

Det kan også brukes for å bestemme ,

, (, )

For å regne ut integralet , kan man anvende delvis integrasjon to ganger.

	,
	,
	,
,	,

 3) Delbrøk oppspaltning   Notater med eksempler

Tre tilfeller vektlegges der er et polynom har lavere grad enn nevneren.

Hvis har høyere grad eller samme grad som nevneren, gjennomfører vi polynom divisjon først.

I)

II)

III)

Analysens fundamental teorem

La være en kontinuerlig funksjon. La F være en funksjon slik at

for all  i . Da gjelder det:

Bestemt integral - oppgaver

 

Uegentlige integraler - Video (Type A (I), Type B( II og III))

I) En eller begge grensene er uendelige - Video 1

II) Diskontinuitet i en av integrasjonsgrensene

III) Diskontinuitet i et eller feller indrepunkt på integrasjonsintervallet

Anvendelser til Integrasjon

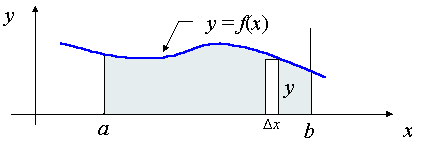
i) Arealregning

Arealet avgrenset av kurven til og -aksen i intervallet er gitt ved: 

Arealet avgrenset av kurven til og -aksen i intervallet er gitt ved: 

ii) Arealet avgrenset av to kurver

Arealet avgrenset mellom grafene til to kontinuerlige funksjoner og er gitt ved:

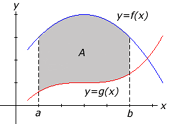
der og er skjæringspunktene mellom grafene.

(er øvre kurven og er nedre kurven. Hvis du er tvil hvilken graf er øvre kurven, kan du bruke , det vil si ta med absoluttverdi)

 

Eksempel.  Bestem arealet avgrenset av grafene til og .

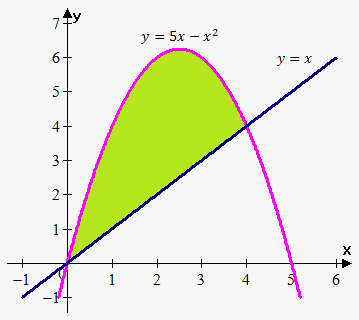Løsning:

 

 

 

 

 

 

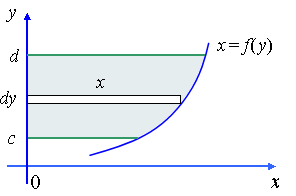
iii) Volumregning

Rotasjon om x-aksen.

Arealet avgrenset av grafen til og -aksen i intervallet roterer en gang om -aksen. Volumet til omdreinings legemet som forekommer er gitt ved:

Rotasjon om y-aksen.

Arealet avgrenset av grafen til og -aksen i intervallet roterer en gang om -aksen. Volumet til omdreinings legemet som forekommer er gitt ved:

iv) Gjennomsnittverdi

Gjennomsnittsverdien til funksjonsverdienes til i intervallet   kan beregnes ved:

v) Buelengde  Notater

Kurvelengden til i intervallet   kan beregnes ved:

         

          Dermed

          

 

 

vi) Arbeid ved integrasjon

Et legeme som er påvirket av en kraft er forflyttet seg fra til . Arbeidet om er utført:

vii) Vanntank

Uegentlig integral  Notat  Video

Oppgaver

Numeriske metoder  -Notater (Trapes- og Midtpunkt-metoden)

Midtpunktsmetode Eksempel -- Video

 

Deriverte til integralfunksjon.

Eksempel:

Arbeid

Video  - Fjær

Arbeidet gjort når væske strømmer inn i en vanntank)

Video 1(kjegleformet-Olje) -  Video 2(synliderformet-vann)