Vektorer i rommet
Vektorer brukes mye i fysikk for å beskrive størrelser som har en bestemt størrelse og en bestemt retning.
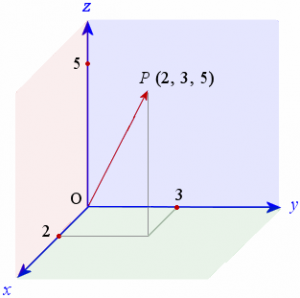
En vektor fra origo til et punkt 
med koodinater kan skrives som:
v = OP = 2 i + 3 j + 5 k .
Mer generell:
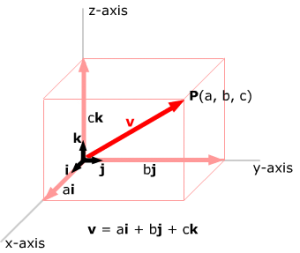
1) Vektoralgebra
- s(u+v)=su+sv der u og v er vektorer og s er reelt tall.
- (s+t)u=su+tu der u og v er vektorer og s og t er reelle tall.
- 1 ·u=u
- (−1)u=−u
- 0 ·u=0 (null vektor)
2) Lengden til en vektor
Lengden til vektoren 
3) Skalarprodukt og vinkelen mellom to vektorer
Skalarprodukt:
der 
er vinkelen mellom vektorene.
Skalarproduktet kan brukes til å bestemme vinkelen mellom to vektorer:
o Hva vil det si når 
?
o Enhetsvektors lang vektoren 
: 
.
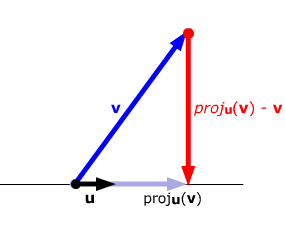
4) Skalarprojeksjon og vektorprojeksjon 
langs 
Skalarprojeksjonen til vektoren 
langs vektoren er lengden til langs :
Vektorprojeksjonen til vektoren langs vektoren er vektor til langs :
Det gjelder:
Vektorprojeksjon - Video 1 - Video 2
Skalar og vektorprojeksjon - Eksempel
Skalar projeksjon er lengden til vektoren langs og vektorprojeksjonen 
er den horisontal komponenten til .
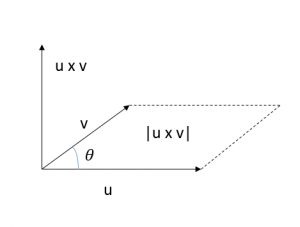
3) Kryssprodukt - Animasjon
o Hva er kryssprodukt og hvordan man kan regne ut det?
o Hvordan kan man regne ut arealet en trekant utspent av to vektorer?
o Hvordan kan man regne ut arealet et parallellogram utspent av to vektorer?
o Retningsvektor, enhetstangentvektor og vektor enhetsnormalvektor
Høyrehånds regelen
5) Ligningen til en rettlinje på parameterframstilling form.
gitt retning vektor 
gjennom et kjent punkt 
:
, 
, 
,
6) Ligningen til et plan:
- gitt normalvektor n=[a, b, c] gjennom et kjent punkt P0(x0,y0,z0):
- gitt tre punkter A, B og C med kjente koordinater.
Man finner normalvektoren 
og velger en av punktene for å sette opp ligningen til planet.
Hvordan kan man bestemme avstanden fra et punkt Q til et plan ved hjelp av skalarprojeksjon?
Det vil si d er skalarprojeksjonen til vektoren PQ langs normalvektoren til planet (video).
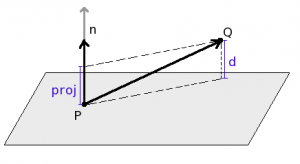
der 
(enhetsvektor langs normalvektoren til planet).