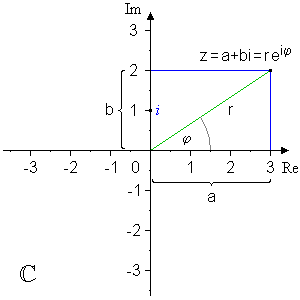Notater og oppgaver m/fasit
Oppsummeringsnotater Se eks. 2.51 (Løsning til z^n=a)
Man må kunne:
Hva er et komplekst tall? Hva er modulen og argumentet for et komplekstall på formen  der
der 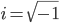 ?
?
Skriv på standardform 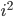 ,
, 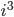 ,
, 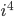 og
og 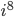 .
.
Forklar kort om komplekst tall på standardform og polarform, og overgangen mellom disse.
Forklar hvorfor når man ganger to komplekstall, argumentet til det nye tallet er summen til argumentene til de komplekse tall?
Hva er kompleks konjugerte(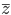 ) til
) til  ? Regn ut
? Regn ut 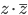 .
.
Hvordan kan man regne ut 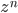 eller
eller 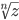 .
.
-----------
Innledning
lærte i MAT100 1t ligningen  har ingen reelle løsninger.
har ingen reelle løsninger.
Nå skal vi utvide vår forståelse og åpne nye dører i den store matematikkensverdenen og definere komplekstall. Vi tar utgangspunkt i definisjonen:
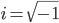 og dermed:
og dermed: 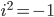 , det vil si:
, det vil si:
 gir
gir 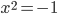 og dermed
og dermed 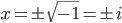 .
.
Et komplekstall kan skrives på standard form, polar form og trigonometriske form henholdsvis:
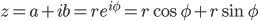
 er den reelle delen og
er den reelle delen og 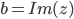 er den imaginære delen.
er den imaginære delen.
der 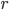 kalles modulen og
kalles modulen og 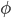 for argumentet:
for argumentet:
Overgangen fra standardform til polarform:
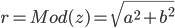 og
og 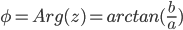
Overgangen fra polarform til standardform:
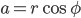 og
og 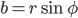
Litt Algebra
Eksempler for å løse ligninger der løsningene er komplekse tall:
Eulers formel
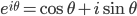
Kan du tenke deg hvordan kan man utlede denne formelen ved hjelp av kjente Macularin rekker?
De Movires formel for å regne ut 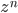 og
og 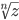
Skriv først 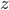 på polarform og deretter kan du regne ut
på polarform og deretter kan du regne ut 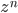 og
og 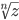 :
:
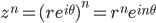 der
der 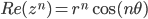 og
og 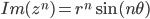
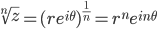 der
der 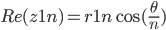 og
og 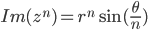
Hva kan kompleksetall brukes til?