Oppsummeringheftet : arbeidsheftet-linalg-MAT10x
(husk at du skal bare sette opp diagonaliseringen og trenger ikke å gange matrisene sammen for å sjekke!)
-----------
1) Hvis 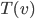 er lineær, hvilke krav skal
er lineær, hvilke krav skal 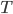 tilfredsstille?
tilfredsstille?
2) Hvis 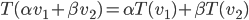 , der
, der  og
og 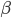 er reelle tall, kan vi
er reelle tall, kan vi 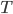 er en lineær transformasjon?
er en lineær transformasjon?
3) Undersøk om transformen 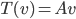 , der
, der 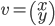 , er lineær for:
, er lineær for:
a) 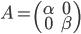
b) 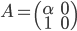
Kontrollspm.
1) Angi egenskapene til en lineær transformasjon $T(v)$?
2) Hvis $T(\alpha v_1+\beta v_2) = \alpha T(v_1)+\beta T(v_2)$, kan vi si $T$ er lineær?
3) La $latex \begin{pmatrix}x'\\ y'\\ z'\\ w'\end{pmatrix}=\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&\cos\theta&-\sin\theta\\ 0&0&\sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}x\\ y\\ z\\ w\end{pmatrix}$