Notater: Konvergenskriterier Oppgaver m/fasit Oppgaver-rekker Oppsummering: Oppsummnotat-rekker
Spørsmål må du kunne vare når du har lest ferdig notatene.
1) Hva er tallfølge og hvilke tallfølger konvergerer?
2) Hva er en uendelig rekke og hva vil det si at en rekke konvergerer?
3) Hvordan kan vi finne ut om en rekke konvergerer eller divergerer?
4) Hva er konvergenstest og forklar litt om konvergenstestene og når og hvordan de kan brukes?
5) Hva er Leibniz-test og når kan brukes?
Tallfølger
Hva er en tallfølge?
Når konvergerer tallfølgen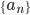 
?
Må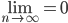 
for at 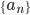skal konvergere?
Rekker
Hva er en uendelig rekke?
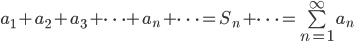
Summen til rekker: Vi skal hovedsakelig ikke bestemme summen i dette kapittelet men vi skal finne om rekken konvergerer eller divererer.
Men vi tar to eksempler her som kan være interessant å se hvordan man kan finne summen:
Bestem summen til en uendelig rekke:
a) Geometrisk rekke: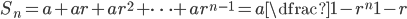 
Dersom kvotienten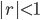 
, konvergerer summen mot 
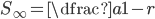Video(eksempel)
b) Teleskoperekker - Video(eksempel)
Konvergens: Hva vil det si at rekken konvergerer?
En uendelig rekke konvergerer dersom summen går mot et endelig bestemt tall: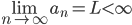 
, der 
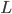er et bestemt tall.
Divergenstest: Video(eksempel)
Hvis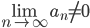 
, så er rekken divergent.
Hvis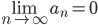 
, så kan rekken konvergere, det vil si rekken kan kanskje konvergere eller kanskje divergere.
Vi kan da velge mellom disse metodene:
I) Foholdstest - Video(teori, eksempler)
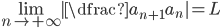
Hvis 
, konvergerer rekken.
Hvis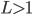 
, divergerer rekken.
Hvis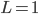 
, kan vi ikke konkuldere noe.
Når brukes forholdstest?
Det brukes vanligvis når man ha eksponentialledd eller fakultetledd i uttrykket.
II) Integraltest - Video(teori, eksempler)
La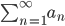 
være en positiv rekke.
La en funksjon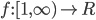 
, med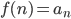 
.
Anta at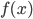 
er avtagende i det minste for 
.
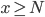Da konvergerer rekken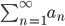 
hvis og bare hvis integralet 
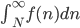konvergerer
Hvis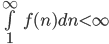 
(konvergerer), så konvergerer 
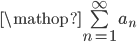også
Hvis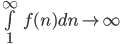 
(divergerer), så divergerer 
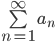også.
Når kan man anvende integraltest?
Integraltest anvendes hovedsakelig når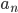 
er integrerbar.
p-rekker - Video(teori, eksempler)
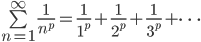
Her kan vi bruke integraltest:
Dermed p-rekken konvergerer for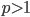 
og divergerer ellers 
.
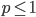III) Sammenligningstest: Video(teori+eksempler)
Hvis den minste av to positive rekker divergerer, så divergerer også den største.
Hvis den største av to positive rekker konvergerer, så konvergerer også den minste.
Hvis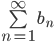 
konvergerer og 
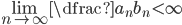, så konvergerer 
også.
Hvis 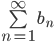divergerer og 
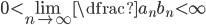, så divergerer også.
Hvis 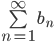konvergerer og 
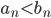, så konvergerer også.
Hvis 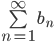divergerer og 
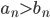, så divergerer også.
---------------------------------------------------------------------------------------------------------------
Leibniz-Kriteriet for alternerende rekker (teori+eksempel, eksempel 2)
Hva er alternerende rekker?
Alternerende rekker er rekker der leddene veksler fortegn, det vil si at annethvert ledd er positivt/negativt.
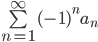
Leibniz’ kriterium for alternerende rekker sier at rekken konvergerer dersom størrelsen på leddene(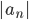
er avtagende, og leddene går mot null:
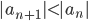for all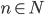 
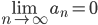
Rottesten, absolutt og betinget konvergens er ikke vektlagt i MAT10x pensum og men vektlagt i MAT112 ved UiB: