Notater med eksempler og oppgaver m/fasit
Inhomogene lineære differensialligninger med konstante koeffisienter
1. orden 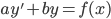
2. orden: 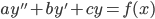
Løsningene til disse to ligningene består av 2 deler, den homogene løsningen og den partikulære løsningen: 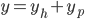 .
.
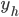 er løsningen til den homogene ligningen og
er løsningen til den homogene ligningen og 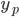 er køsningene til den inhomogene løsningen.
er køsningene til den inhomogene løsningen.
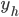 (den homogene løsningen):
(den homogene løsningen):
Homogene lineære differensialligninger med konstante koeffisienter
1. orden: 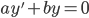
Ved å anta 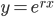 er en løsning, kan man sette opp den karakteristiske ligningen:
er en løsning, kan man sette opp den karakteristiske ligningen:
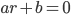
2. orden: 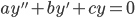
Ved å anta 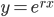 er en løsning, kan man sette opp den karakteristiske ligningen:
er en løsning, kan man sette opp den karakteristiske ligningen:
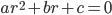

Den partikulære løsningen kan bestemmes ved å velge 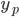 med å ta utgangspunkt i
med å ta utgangspunkt i 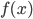 :
:
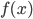
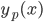
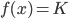 gir
gir 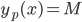
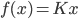 gir
gir 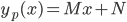
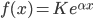 gir
gir 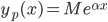
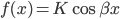 gir
gir 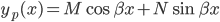
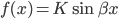 gir
gir 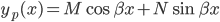
Legg merke til hvis det innhomogene leddet er samme som den homogene løsningen, har man har dobbelløsning, skal man gange 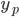 med
med 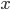 eller kanskje med
eller kanskje med  hvis
hvis 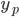 er trippelløsning.
er trippelløsning.
Eksempel:
For 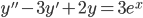 er den homogene løsningen
er den homogene løsningen 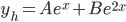 og dermed
og dermed 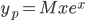 . (her er
. (her er 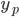 døbbelløsning)
døbbelløsning)
For 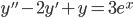 er den homogene løsningen
er den homogene løsningen  og dermed er
og dermed er 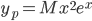 . (her er
. (her er 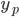 trippelløsning)
trippelløsning)